Features and Functionalities¶

Where to find simulation LOG file¶

The simulation log file is a file with the same name as the input file and the extension *.log. It is located in the output folder of the simulation. It is necessary for the support team to debug issues with the simulation, thus it should always be attached to a support request. Please also include additional debug information in case the log file shall be used for support, refer to How can I add additional debug information to the LOG file?.

What is the difference between nextnano³ and nextnano++?¶

The short answer is: Use nextnano++.

This is the tool where we put on most effort in improving it by adding new features. The nextnano³ tool is mainly distributed for historical reasons.

The nextnano³ tool is written in Fortran. It has been developed at the Walter Schottky Institute from 1999 to 2010. The nextnano++ tool is written in C++. It has been developed at the Walter Schottky Institute from 2004 to 2008. The tools have been written by different people that were working at the Walter Schottky Institute of the Technische Universität München in the Theoretical Semiconductor Physics group of Prof. Peter Vogl.

Essentially, both tools cover the same physics and methods, namely

the strain equation
the Poisson equation
the Schrödinger equation
the drift-diffusion current equation.

Additionally, nextnano³ includes

solar cells
electrolytes
graphene
tight-binding (for bulk and one-dimensional superlattices)
the self-consistent CBR method (1D, 2D and 3D)
the NEGF method (1D only) which is particularly suited for quantum cascade lasers.

In contrast to nextnano++, nextnano³ is not able to

treat the magnetic field within the $\mathbf{k} \cdot \mathbf{p}$ approach
calculate the g tensor
include quaternary materials.

The nextnano++ tool is much faster for drift-diffusion calculations and for 2D/3D simulations. For instance, if you work on LEDs, MOSFETs or Quantum Dots, nextnano++ is much better suited.

There are some applications where it is irrelevant which tool to use. In this case we recommend to use both. This has the advantage that the results of one tool can be compared to the results of the other one in order to gain more confidence in them. For some applications, one tool should be preferred. Please contact <support[at]nextnano.com> to find out which tool to choose for your particular application.

nextnano³ syntax

‘’$’’ character for the keywords: $regions ... $end_regions
‘’%’’ character for the variables: %QuantumWellWidth = 5.0
‘’!’’ character for comments: ! This is a comment. (# is supported by both nextnano and nextnano³ as a comment sign.)

nextnano++ syntax

‘’{}’’ brackets for the keywords: structure{ ... }
‘’$’’ character for the variables: $QuantumWellWidth = 5.0`
‘’#’’ character for comments: # This is a comment. (# is also supported by nextnano³.)

Can I convert nextnano³ input files into nextnano++ input files?¶

Within nextnanomat, there is an experimental feature to convert a nextnano³ input file to a nextnano++ input file. How to use this automatic conversion:

In the menu select Tools ==> Convert nextnano³ input file to nextnano++

When you use the automatic conversion of nextnano³ input file into nextnano++, you will find that it probably does not work completely.

If you save and run the nextnano++ input file that has been converted and that has the suffix _nnp.in, very likely some errors appear indicating which line(s) to change. Then some manual adjustments are needed, but the rough structure should help a lot for the conversion.

How can I track how much memory is used during the simulations?¶

See How can I add additional debug information to the LOG file?.

Can I pass additional command line arguments to the executable?¶

See Can I pass additional command line arguments to the executables of simulation tools?.

How can I speed up my calculations with respect to CPU time?¶

The most obvious way is to reduce the number of grid points you are using. For instance, for the following p-n junction simulation, a grid spacing of 1 nm was used (gray lines in Figure 2.11.1 ). If one is using a coarse grid of only 10 nm, the calculated values (squares in Figure 2.11.1) agree very well with the calculated values of the thin lines.

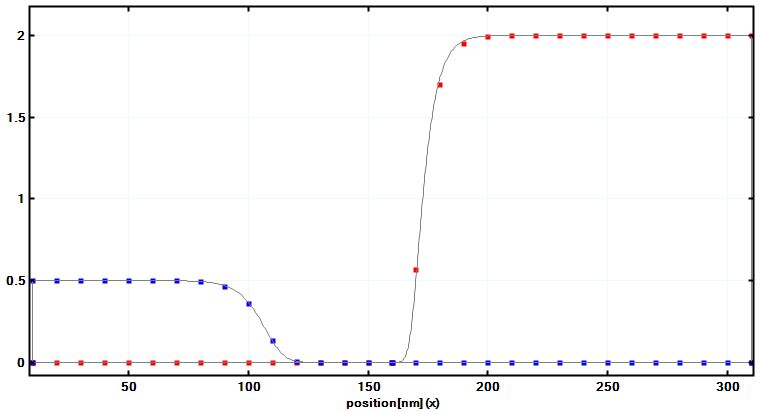
../../../_images/FAQ_pn_junction_coarse_grid_densities.jpg — Figure 2.11.1 Hole (blue) and electron (red) densities of the p-n junction in units of $10^{18} cm^{-3}$. The gray lines are from simulations using a 1 nm grid spacing. The squares are from a simulation that uses only a 10 nm grid resolution. Note that the center coordinate of this plot is x=160 nm. The depletion width for the holes is around wp:math:approx`50 nm, for the electrons it is wn:math:approx`10 nm which is of the order of the grid spacing. Even in this case, the calculated electron density is reasonably accurate.¶

The difference in CPU time comes from the fact that for the 10 nm resolution the dimension of the matrix that is used for discretizing the Poisson equation is 30, while in the case for the 1 nm grid spacing it has the dimension 300. The proper choice of an optimal grid spacing is very relevant for 2D and 3D simulations, as can be seen in the following.

1D simulation (length of sample: x = 300 nm)

1 nm grid spacing: dimension of Poisson matrix: $N=300$
10 nm grid spacing: dimension of Poisson matrix: $N=30$

2D simulation (length of sample: x = 300 nm, y = 300 nm)

1 nm grid spacing: dimension of Poisson matrix: $N=300 \cdot 300 = 90,000$
10 nm grid spacing: dimension of Poisson matrix: $N=30 \cdot 30 = 900$

3D simulation (length of sample: x = 300 nm, y = 300 nm, z = 300 nm)

1 nm grid spacing: dimension of Poisson matrix: $N=300 \cdot 300 \cdot 300 = 27,000,000$
10 nm grid spacing: dimension of Poisson matrix: $N=30 \cdot 30 \cdot 30 = 27,000$

If a quantum mechanical simulation is performed, the numerical effort of eigenvalue solvers increases with the number of grid points $N$ with order $O\left(N^2\right)$.

Can I take advantage of parallelization of the nextnano software on multi-core CPUs?¶

The short answer is:

Some numerical routines are parallelized which is done automatically. These are the numerical routines, e.g. for calculating the eigenvalues with a LAPACK solver (which itself uses BLAS).

The long answer is:

The nextnano software includes the Intel® Math Kernel Library (MKL). MKL includes the BLAS and LAPACK library routines for numerical operations. The MKL dynamically changes the number of threads.

nextnano++ - uses MKL (parallel version). The executables that are compiled with the Intel and Microsoft compilers use MKL (parallel version). The executable that is compiled with the GNU compiler (gcc/gfortran) uses the nonparallelized version of the BLAS and LAPACK source codes available from netlib webpage.
nextnano³ - uses MKL (parallel version) The executables that are compiled with the Intel and NAG (64-bit) compilers use MKL (parallel version). The executables that are compiled with the GNU compiler (gfortran) and NAG (32-bit) use the nonparallelized version of the BLAS and LAPACK source codes available from netlib webpage. There is a nextnano³ executable available that uses OpenMP parallelization for
- CBR (parallelization with respect to energy grid)
- NEGF (parallelization with respect to energy grid and further loops) number-of-MKL-threads = 8
- Calculation of eigenstates for each $k_\parallel$ (1D and 2D simulations)
- Matrix-vector products of numerical routines Note: Not all operations are thread-safe, e.g. one cannot combine $k_\parallel$ parallelization with the ARPACK eigenvalue solver. Only for this executable, the flag number-of-parallel-threads = 4 has an effect. The NEGF keyword also supports number-of-MKL-threads = 4 (0 means dynamic with is recommended) and MKL-set-dynamic = yes / no.
nextnano.NEGF - uses MKL (parallel version)
nextnano.MSB - uses MKL (parallel version)

The NEGF algorithms (nextnano.NEGF, nextnano.MSB, CBR) include matrix-matrix operations which are well parallelized within the BLAS routines.

If e.g. 4 nextnano simulations are running in parallel on a quad-core CPU, i.e. 4 nextnano executables are running simultaneously and each of them is using calls to the parallelized MKL library simultaneously, the total performance might be slower compared to running these simulations one after the other. In this case using a nextnano executable compiled with the serial version of the Intel MKL could be faster.

In fact, it strongly depends on your nextnano application (e.g. 1D vs. 3D simulation, LAPACK vs. ARPACK eigenvalue solver, …) if you benefit from parallelization or not. In general, the best parallelization can be obtained if you run several nextnano simulations in parallel. For instance, you could do parameter sweeps (e.g. sweep over quantum well width) using nextnanomat’s Template feature, i.e. if you run 4 simulations simultaneously on a quad-core CPU, e.g. for 4 different quantum well widths.

What boundary conditions are available?¶

There are three different boundary conditions that we use:

periodic: $\psi(x=0) = \psi(x=L)$
Dirichlet: $\psi(x=0) = \psi(x=L) = 0$, and
Neumann: $\frac{\text{d}\psi}{\text{d}x} = \text{const}$ at the left ($x=0$) and right ($x=L$) boundary. Typically, $\text{const} = 0$.

By specifying both Dirichlet and Neumann boundary conditions, the system would be over-determined.

What are quasi-Fermi levels¶

So-called quasi-Fermi levels which are different for electrons $E_\text{F,n}$ and holes $E_\text{F,p}$ are used to describe non-equilibrium carrier concentrations. In equilibrium the quasi-Fermi levels are constant and have the same value for both electrons and holes, $E_\text{F,n}=E_\text{F,n}=0\text{ eV}$. The electron current is proportional to the electron mobility $\mu_\text{n}(x)$, carrier density $n(x)$ and the gradient of the quasi-Fermi level of the carriers, $\nabla E_\text{F,n}(x)$, and analogously for the holes.

I do not understand the $\mathbf{k} \cdot \mathbf{p}$ parameters¶

In the literature, there are two different notations used:

Dresselhaus–Kip–Kittel (DKK): $L, M, N^+, N^-$ (zinc blende); $L_1, L_2, M_1, M_2, M_3, N_1^+, N_1^-, N_2^+, N_2^-$ (wurtzite)

Luttinger parameters: $\gamma_1, \gamma_2, \gamma_3, \kappa$ (zinc blende); Rashba–Sheka–Pikus (RSP) parameters $A_1, A_2, A_3, A_4, A_5, A_6, A_7$ (wurtzite)

They are equivalent and can be converted into each other.

Some authors only use 3 parameters $L, M, N$ (or $\gamma_1, \gamma_2, \gamma_3$) which is fine for bulk semiconductors without magnetic field but not for heterostructures because the latter require 4 parameters, i.e. $N^+, N^-$ (instead of $N$ only) or $\kappa$. If these parameters are not known, they can be approximated.

There are different $\mathbf{k} \cdot \mathbf{p}$ parameters for

6-band $\mathbf{k} \cdot \mathbf{p}$ and

8-band $\mathbf{k} \cdot \mathbf{p}$.

The 8-band $\mathbf{k} \cdot \mathbf{p}$ parameters can be calculated from the 6-band parameters taking into account the temperature dependent band gap $E_{\rm gap}$ and the Kane parameter $E_{\rm P}$ (zinc blende). For wurtzite the parameters are $E_{\rm gap}$ and the Kane parameters $E_{{\rm P}1}$, $E_{{\rm P}2}$.

The 8-band Hamiltonian also needs the conduction band mass parameter $S$ (zinc blende) or $S_1, S_2$ (wurtzite). They can be calculated from the conduction band effective mass $m_{\rm c}$, the band gap $E_{\rm gap}$, the spin-orbit split-off energy $\Delta_{\rm so}$ and the Kane parameter $E_{\rm P}$ (zinc blende). For wurtzite the parameters are $m_{{\rm c},\parallel}$, $m_{{\rm c},\perp}$, $E_{\rm gap}$, $\Delta_{\rm so}$, the crystal-field split-off energy $\Delta_{\rm cr}$ and the Kane parameters $E_{{\rm P}1}$, $E_{{\rm P}2}$.

Finally there is the inversion asymmetry parameter $B$ for zinc blende. For wurtzite there are $B_1, B_2, B_3$.

For more details on these equations, please refer to Section 3.1 The multi-band $\mathbf{k} \cdot \mathbf{p}$ Schrödinger equation in the PhD thesis of S. Birner.

Spurious solutions

Some people rescale the 8-band $\mathbf{k} \cdot \mathbf{p}$ in order to avoid spurious solutions. The 8-band $\mathbf{k} \cdot \mathbf{p}$ parameters can be calculated from the 6-band parameters taking into account the band gap $E_{\rm gap}$, the spin-orbit split-off energy $\Delta_{\rm so}$ and the Kane parameter $E_{\rm P}$ (zinc blende). For wurtzite the parameters are $E_{\rm gap}$, the spin-orbit split-off energy $\Delta_{\rm so}$, the crystal-field split-off energy $\Delta_{\rm cr}$ and the Kane parameters $E_{{\rm P}1}$, $E_{{\rm P}2}$.

For more details, please refer to Section 3.2 Spurious solutions in the PhD thesis of S. Birner.

Specific implementation nextnano++

See section quantum{ region{ kp_8band{} } } in Multi-band models in quantum{ region{ } }.

Specific implementation nextnano³

See section Choice of $\mathbf{k} \cdot \mathbf{p}$ parameters in $numeric-control.
See section $\mathbf{k} \cdot \mathbf{p}$ parameters in Which material parameters are used?.
See section Luttinger-parameters in $binary-zb-default.

Can I add new materials to the database?¶

Sure!

Option 1

The material parameters are contained in ASCII text files. You can find them in the installation folder:

nextnano³ tool: C:\Program Files (x86)\nextnano\<date>\nextnano++\Syntax\database_nnp.in

nextnano++ tool: C:\Program Files (x86)\nextnano\<date>\nextnano3\Syntax\database_nn3.in

These files can be edited with any text editor, such as Notepad++.

It is best if you search for a material such as ‘’GaSb’’ and then simply use ‘’Copy & Paste’’ to reproduce all relevant entries and then you rename ‘’GaSb’’ to something like ‘’GaSb_test’’. Finally, you adjust the necessary material parameters that you need. In most cases, you do not have to replace all material parameters. It is only necessary to replace the ones that you need in the simulation.

It is a good idea to save the new database to a new location such as

C:\Users\<user name>\Documents\nextnano\My Database\database_nnp_GaSb_modified.in You can then read in the new nextnano++ (or nextnano³) database specifying the location within the Tools Options of nextnanomat.

Tools => Options... => Material database => nextnano++/nextnano³ database file:

Option 2

A quicker way is the following. You can overwrite certain material parameters in the input file rather than entirely defining new materials. For instance if you need ‘’HfO2’’, you could use the material ‘’SiO2’’ and just change the static dielectric constant and conduction and valence band edges or any other relevant parameters that you need. So basically, you are using the material ‘’SiO2’’ a modified static dielectric constant and band edges.

Please note that we treat all materials to be either of the crystal structure

zinc blende (including diamond type) or

wurtzite.

Attention

More information on how to add materials

to nextnano++ can be found in Material Database
to nextnano³ can be found on How to add material parameters.

Should I use averaged outputs and boxes?¶

The averaged = yes is similar to boxes = no. Note that boxes is related to output of material grid points while averaged is related to output of simulation grid points.

2D and 3D simulations can produce a lot of output data (order of GB). It is strongly recommended to use averaged = yes for 2D and 3D simulations to avoid excessive consumption of your hard disk.

Last update: 23/10/2024